1. 问题

问题同《》，这个例子并不是特别恰当，当在于简单，数字小，方便验证，方便理解，特别是计算概率的部分。

设有10个非负整数，用不多于20个的储存单元来存放，如何存放这10个数，使得搜索其中的某一个数时，在储存单元中查找的次数最少？

问题类似于，有10个带号码的球，放到编号为{0, 1, 2, …, 19}共20个盒子中，每个盒子最多放一个，问如何放，使能够用最少的次数打开盒子，知道任一个球所在的盒子编号？

 

2. 分析

《》中，我们提到用单散列算法来解决冲突，比简单散列算法冲突的比率有所降低，但18%的冲突率，对于实际应用来说还是略偏高，《初等数论及其应用》中，说明是从另一个角度来说明该冲突率高的原因。

设 h₀(k) ≡ k (mod m), k = 球号， m = 盒子数量

h_j(k) ≡ h₀(k) + j，0<= j < m,  h_j(k) 表示发生 j 次冲突后，球所放入的盒子编号

∴ h_j+1(k) ≡ h₀(k) + (j + 1) ≡ h_j(k) + 1

∴ 只要有一个h_i(k₁) ≡ h_j(k₂)

则所有的h_i+n(k₁) ≡ h_j+n(k₂) (n = {0, 1, 2, …})

用数学归纳法可以很容易的证明

也可以用同余算法如下证明:

h_i+n(k₁) ≡ h₀(k₂) + n

∵ h_i(k₁) ≡ h_j(k₂)

∴ h_i+n(k₁) ≡ h_j(k₂) + n ≡ h_j+n(k₂)

∴ 只要有一个球对应的盒子编号h_i(k₁)与另一个h_j(k₂)冲突，则会有无数对 h_i(k₁)+n 和 h_j(k₂)+n  冲突

如《》测试的数据中，0和19冲突，则 0+1 = 1 和 19+1 = 20也是冲突的，类似, 2和21， 3和22等等都会冲突，也就是说，只要球号中有对应的连续数列，就特别容易产生冲突，导致该序列查找的次数会剧增，这个问题称为”clustering”，书中《初等数论及其应用》中翻译为堵塞，我觉得翻译为聚集冲突更合适，这是因为简单的加1不能使数字不能足够分散所致。

这里用一组聚集冲突的数据演示一下：

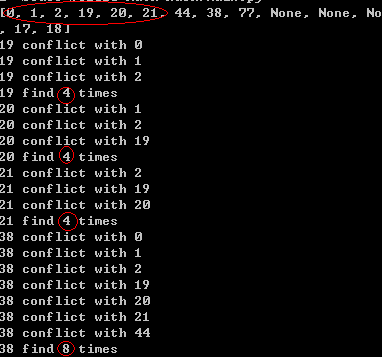
numList = [0, 1, 2, 19, 20, 21, 18, 44, 17, 38, 77];

测试结果发现，所有的连续数列的球号都排在前8个序号的盒子中，冲突的序列都需要4次的查找，而38因为和连续数列的第一个数字同余冲突，导致的查找次数更是达到8次，如果散列函数处理的数据中有如此的序列，那么算法性能会急剧下降。

 

为了解决这个问题，既然有单散列算法，那么自然就想到双散列算法。

 

3. 双重散列算法

双散列算法为了解决单散列算法中 +j 过于连续，不够分散而来，同时能够进一步降低冲突率。其为了进一步分散冲突的数字，对冲突的球的数字再一次进行散列

h₀(k) ≡ k (mod m), k = 球号

m = 盒子的数量，m 取接近最大盒子数量的素数

散列函数1 : g(k) ≡ k + 1 (mod m -2)

散列函数2 : h_j(k) ≡ h₀(k) + j*g(k) (mod m),  h_j(k) 表示发生 j 次冲突后，球所放入的盒子编号

注意g(k)的模变了，变为 (m-2)，为什么要用这个，一会分析冲突要用

 

4.双重散列生成示例

仍用《》中的测试数据{0, 1, 2, 7, 9, 15, 19, 20, 77, 38}

m = 19, m-2 = 17

球号	0	1	2	7	9	15	19	20	77	38
模19余数	0	1	2	7	9	15	0	1	4	0

分配前6个球时没有冲突，分配如下：

盒子编号	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
球号	0	1	2					7		9						15

当分配到第7个球19时，h₀(19) ≡ 0 (mod 19), 需要放到编号为0的盒子，此时产生第一次冲突计算h₁(k)

g(k) ≡ g(19) ≡ 19 + 1 ≡ 3 (mod 17)

h₁(19) ≡ h₀(19) + 1*g(19) ≡ 0 + 1*3 ≡ 3 (mod 19)

所以19该放至编号为3的盒子，该盒子为空，不冲突，放入即可。

类似的，可以求到前9个球放入的盒子的位置，都只有一次冲突：

盒子编号	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
球号	0	1	2	19		20		7		9		77				15

当分配最后一个球38时，h₀(38) ≡ 0 (mod 19), 第一次冲突

g(38) ≡ 38 + 1 ≡ 5 (mod 17)

h₁(38) ≡ h₀(38) + 1*g(38) ≡ 5 (mod 19)，发现扔和20号球冲突，进一步计算h₂(k)：

h₂(38) ≡ h₀(38) + 2*g(38) ≡ 10 (mod 19)，无冲突

通过整个上述散列函数计算过程，最终的散列值经过再次散列与冲突的次数 j 相乘后，最终的分配都比较分散，间隔相对均匀，因此冲突数显著减少

 

5. 双重散列函数聚集冲突问题

若双重散列函数要发生聚集冲突，则

若双重散列函数h_i(k₁)与另一个h_j(k₂)冲突（k₁ != k₂），且有h_i+1(k₁) 和  h_j+1(k₂) 冲突时：

∵ h_i(k₁) ≡ h_j(k₂)

∴ h_i(k₁) ≡ h₀(k₁) + i*g(k₁) ≡ h_j(k₂) ≡ h₀(k₂) + j*g(k₂)

∴ h₀(k₁) + i*g(k₁) ≡ h₀(k₂) + j*g(k₂)                      ①

同理：

∵ h_i+1(k₁) ≡ h_j+1(k₂)

∴ h₀(k₁) +（i+1）*g(k₁) ≡ h₀(k₂) + (j+1)*g(k₂)          ②

根据同余算法，②减①得：

g(k₁) ≡ g(k₂)   (mod m)

∵ 0 < g(k) < m – 2

∴ g(k) 都为最小余数

∴ g(k₁) = g(k₂)

∴ k₁ + 1  ≡ k₂ + 1 (mod m-2)

∴ k₁  ≡ k₂  (mod m-2)                                          ③

 

Rosen的《初等数论及其应用》第6版207页给出了该证明，但为了证明双重散列函数没有单散列函数的”clustering”问题，也就是书中所翻译堵塞问题（我觉得翻译有误，按照说明更合适的翻译应该是集中或聚集问题，即一段有序的数列一旦有一个数和另一段有序数列冲突，则会2段序列中后续的数列都会冲突，导致查找步骤急剧增加），其接着说如果上述条件成立，则可简化同余式①，得：

h₀(k₁)  ≡ h₀(k₂) (mod m)

即：k₁  ≡ k₂  (mod m)

从而得出，在 m(m-2)内只有唯一的一个解得结论，即不会有冲突

我尝试证明这个省掉的步骤未果，但却找到一个反例了，我给该书的作者Rosen写了封邮件，但一直没回我，如看帖的朋友能补齐该证明请告诉我。

反例：当m = 19, m-2 = 17时：

设k₁ = 1, k₂ = 18

∴ h₀(k₁) = 1， h₀(k₂) = 18 (mod 19)

∴ k₁  ≡ 1 ≡ k₂  ≡ 18   (mod 17) , 满足同余③

同余式①:

h₀(k₁) + i*g(k₁) ≡ 1 + i     (mod m = 19)

h₀(k₂) + j*g(k₂)  ≡ 18 + j                

易知：当 i  = 0, j = 2时，他们成立（1 ≡ 20）

但1  ≡ 18  (mod 19) 并不成立

 

但是如果加一个条件： i = j

∵ g(k₁) = g(k₂)

∴ i*g(k₁) = j*g(k₂) 

∴ h₀(k₁)  ≡ h₀(k₂) (mod m)

即：k₁  ≡ k₂  (mod m)

根据中国剩余定理，只同时满足：

k₁  ≡ k₂  (mod m-2)

k₁  ≡ k₂  (mod m)

当m 和 m -2互素时，公式 x ≡ a (mod m-2), x ≡ a (mod m) 在 m(m-2)的范围内有且只有一个唯一解:

即: k1 = k2   (k < m(m-2))

所以在m(m-2)范围内不会有2个数k₁, k₂模m冲突的情况下，又有h_j(k) ≡ h₀(k) + j*g(k) (mod m)再次冲突

但是仍然会发生，k₁, k₂模m冲突，且h_j(k)又和另一个k₃冲突的情况。

 

6. 双重散列函数冲突概率问题

为了简单，我们仍然只考虑在h₀(k)冲突时，h₁(k) ≡ h₀(k) + 1*g(k) (mod m)再次冲突的概率：

仍设最大的球号为 s：

1> 由第5部分的证明知，当 s < m(m-2))时，这种冲突概率为0

2> 当 s > m(m-2)时，设k为第一个球的球号

根据中国剩余定理知，其他解 k_x ≡ k (mod m(m-2))，会满足：

k_x  ≡ k  (mod m-2)

k_x  ≡ k  (mod m)

即会产生h₀(k)和h₁(k)的同时冲突，其概率为每m(m-2)个数内会出现一次

故其冲突概率 = 1/m(m-2)

当m = 19时，冲突概率 = 0.31%，这个概率明显要比简单散列函数和单散列函数要低得多，所以双重散列函数的冲突率是非常低的

 

7. python code 和演示结果

1 m = 19;         #m -2 = 17, is a prime number 2  3 #g(k) = (k + 1) % (m - 2) 4 #h(k) = k % m 5 #hj(k) = h(k) + j*g(k) 6 def DoubleHash(numList): 7     if len(numList) > m: 8         print "num list len is :", len(numList), "is big than mod :", m; 9         return None;10 11     hashList = [None] * m;12     for k in numList:13         for j in range(m):14             g_k = (k + 1) % (m - 2);15             hj_k = (k + j * g_k) % m;16             if None == hashList[hj_k]:17                 hashList[hj_k] = k;18                 break;19         else:20             print "num list is too big, hash list is overflow";21             return None;22 23     return hashList;24     25 def CheckDoubleHash(numList, hashList):26     if None == hashList:27         return;28 29     for k in numList:30         for j in range(m):31             g_k = (k + 1) % (m - 2);32             hj_k = (k + j * g_k) % m;33             #check the key is equal with the one in hash list, if not check the next one34             if hashList[hj_k] == k:35                 if j > 0:36                     print k, "find", j+1, "times";37                 break;38             else:39                 print k, "conflict with", hashList[hj_k]; 40         else:41             print k, "is not find...";42             return False;43 44     return True;

 

测试时，设置了m = 19

测试数列为: numList = [0, 1, 2, 7, 9, 15, 19, 20, 77, 38]，为了测试冲突，故意设置了一些冲突数，为了减少无用的输出，对于没有冲突的就不打出了，测试结果如下：

只有38在发生了冲突1次，而且，所有的球号分散相对单散列函数分布要分散得多，说明双重散列函数分散效果均匀性更好，从而冲突率是非常低的

同时，注意，实际上38 < 17*19， 仍然发生冲突了，原因就是38和0冲突后，h₁(38) = 20，又和20冲突，从而导致其最终经过双重散列后仍有冲突

 

再看下双重散列函数对第2部分的聚集冲突的连续数列处理结果：

numList = [0, 1, 2, 19, 20, 21, 18, 44, 17, 38, 77];

可以发现，冲突大大减少，没有高于3次的查找，且连续数列{19, 20, 21}被分散开来，有效的减少了单散列函数聚集冲突问题